Abstract
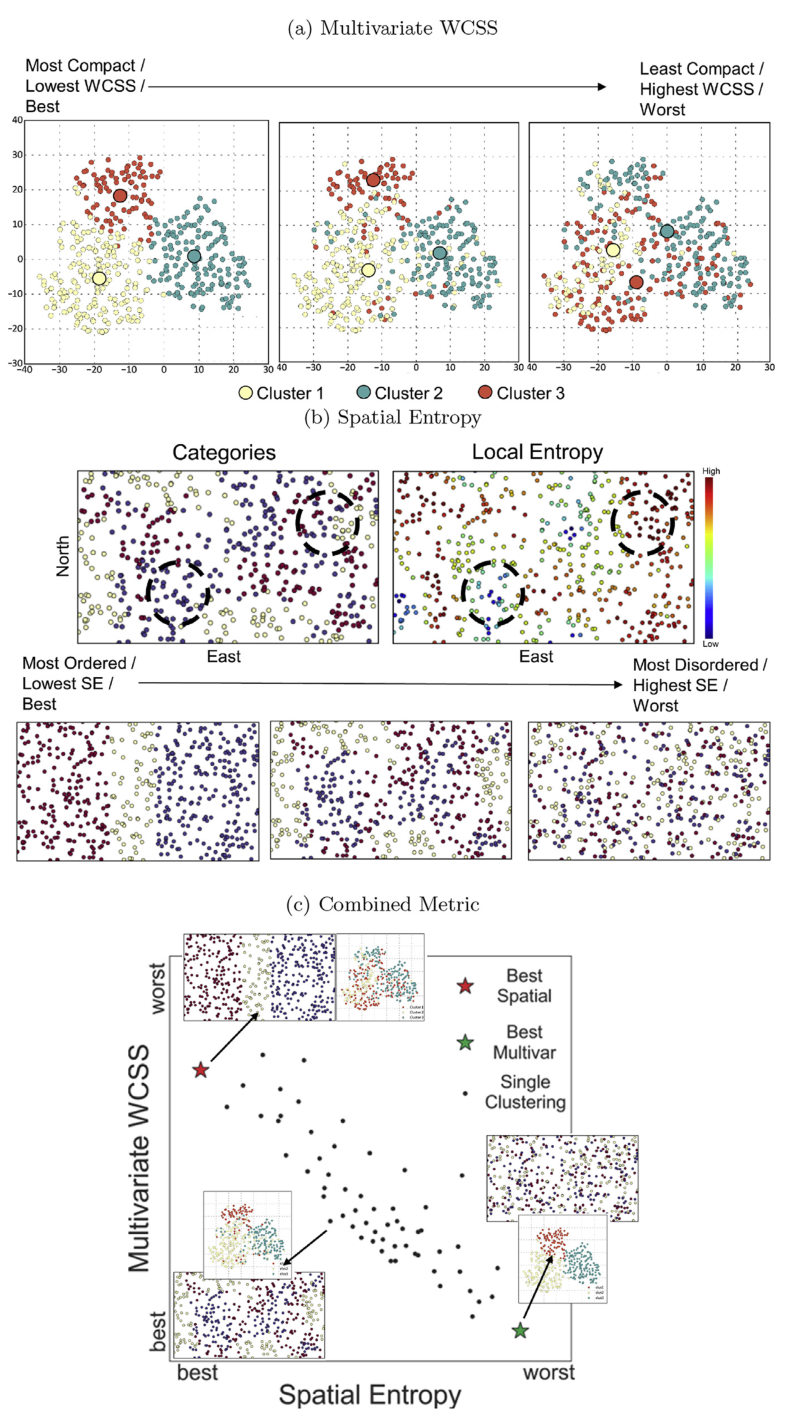
The subdivision of samples into stationary sets is one of the first decisions in a resource modeling workflow where geologically and statistically related samples are grouped for further geostatistical modeling. Unsupervised learning algorithms (clustering) with modifications to consider spatial correlation have several benefits in the decision of stationarity, they are: automatic and repeatable; assess uncertainty; and provide a framework for checking existing groupings. However, subjective parameterization remains a critical limitation for the application of spatial clustering in geostatistical workflows. In this work, two main extensions to the current state of research are proposed: 1) a combined spatial-multivariate metric that describes cluster quality in both multivariate and Cartesian space by measuring multivariate compactness and spatial contiguity; and 2) a novel random-path spatial-multivariate ensemble clustering algorithm to reduce the reliance on subjective clustering parameterization. The metrics developed in this work quantify clustering quality based multivariate and spatial properties. Moreover, the proposed clustering algorithm allows the user to control the spatial contiguity and multivariate compactness of the final clusters by modifying a single parameter. The clustering algorithm is introduced and demonstrated on a synthetic test dataset, then further application to more complex datasets are explored to demonstrate the clustering properties and simplicity of tuning the algorithm to prefer spatially contiguous clusters or multivariate compactness. The proposed algorithm outperforms other clustering algorithms for the datasets tested based on the metrics developed.